泛克里金插值法的原理及其应用
# 1.引言
普通克里金法要去区域化变量是二阶平稳或者内蕴的,至少是准二阶或者准内蕴的。在此条件下,至少在估计领域内有
(常数),即期望为常数。然而实际中,许多区域化变量
在估计领域内是非平稳的,即
,这时就不能用普通克里金方法进行估计,而是要采用泛克里金法进行估计。
# 2.泛克里金原理
# 2.1泛克里金法的定义
所谓泛克里金,就是在漂移的形式和非平稳随机函数
的协方差函数
或变异函数
为已知的条件下,一种考虑到有漂移的无偏线性估计量的地统计学方法,这种方法属于线性非平稳地统计学范畴。
# 2.2 漂移和涨落
# 漂移
漂移定义为非平稳区域化变量的数学期望,在任一点
上的漂移就是该点上区域化变量
的数学期望。其表达式为:
漂移比较复杂,不能用简单分析表达式来模拟整个样品域,经常用领域模型来研究。在给定的以点为中心的领域内的任一点,其漂移
可用如下函数表示:
式中,为一已知函数;
是未知系数。
通常采用多项式形式,在二维条件下,漂移可看成坐标
的函数。
# 涨落
对于有漂移的区域化变量,假设可分解为漂移和涨落两部分,如下所示:
式中,为点
处的漂移,
称为涨落。那么,区域化变量
的分解可以这样理解:
由两个不同尺度的现象合成,
是在较大尺度下可以观察的现象变化,
是在较小尺度下的现象变化。由此可得到:
所以,可见,涨落是一个数学期望为0的区域化变量,可认为涨落是围绕漂移
摆动的随机误差。
# 2.3 非平稳区域变量的协方差函数和变异函数
# 2.3.1 基本假设
假设的增量
具有非平稳的数学期望
和非平稳的方差函数,即假设下式存在:
# 2.3.2 协方差和变异函数
当时,
的协方差函数
为:
即,说明
的协方差函数就等于涨落
的协方差函数
。
的变异函数
为:
即,说明
的变异函数就等于涨落
的变异函数
# 2.4 的克里金法估计
的克里金法估计
由于多为未知,故不能基于原始数据用
来计算
。因此泛克里金估计有两方面的内容,一是
的估计,二是
的估计。由于泛克里金法比较复杂,本文仅简单解释
的估计问题。
设为一非平稳区域化变量,其数学期望为
,协方差函数为
且已经,则:
设的漂移
可表示为如下
个单项式
的线性组合
已知个样点
,其观测值为
,现要用这些样点估计领域内任一点
的值
,
的泛克里金估计量为:
为使得为
的无偏最优估计量,需要在以下两个条件下求解权重系数
。
# 2.4.1 无偏性条件
若要满足无偏性条件,需,则
即对任一组系数等式均成立,需
成立。这个子式称为无偏性条件。
# 2.4.2 最优性条件
在满足无偏性条件下,用估计
的泛克里金估计方差为:
将无偏性条件带入,可得到
要求在满足无偏性条件下,使得估计方差最小的权重系数。
需要根据拉格朗日乘数法原理,建立拉格朗日函数。
求出函数对
个权系数
的偏导数,并令其为0,并和无偏性联立建立如下方程组。
整理得到估计的泛克里金方程组:
从泛克里金方程组可以得到以下两等式:
将等式带入估计方差公式,可得到泛克里金方法,记为。
用变异函数表示泛克里金方程组如下:
写成线性方程组的形式就是:
写成矩阵的形式即为:
对矩阵求逆即可求解和
用变异函数表示泛克里金方差如下:
# 3.泛克里金法案例应用
假设某一区域气温是非平稳的区域化变量,在南北方向(空间坐标的方向)上存在线性漂移,即
。若已知其涨落满足二阶平稳假设,并且拟合的协方差函数模型为球状模型,如下所示:
利用泛克里金对下表中的0号点进行估计。
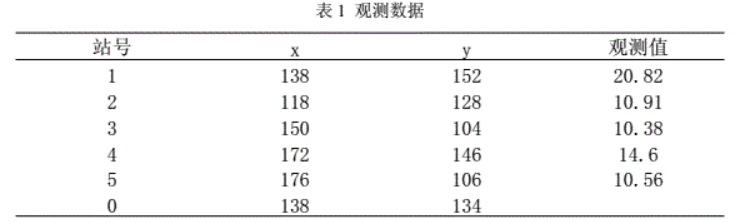
# 3.1 漂移基函数元素的计算
由于漂移为。
时,
,因此
时,
,因此
那么有
# 3.2 两点之间距离和协方差函数
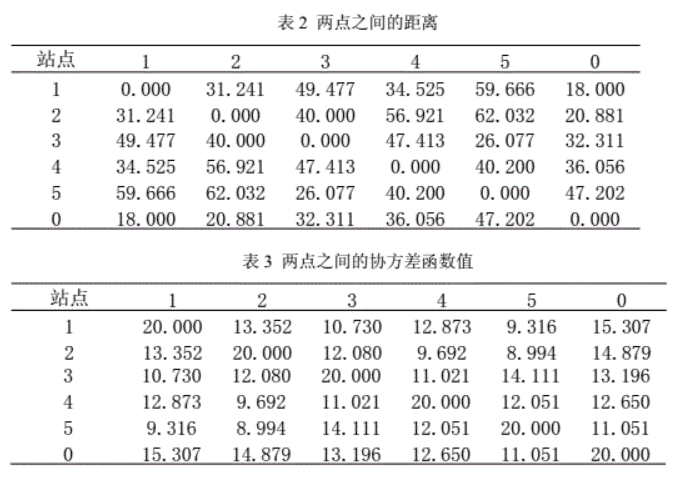
# 3.3经计算得到泛克里金方程组矩阵
根据2.4.2,列出泛克里金方差组矩阵
泛克里金方程组即体现距离关系(协方差衡量),又体现了非平稳特性(漂移函数)。
通过矩阵运算,求解得到
# 3.4 计算结果
将权重值带入泛克里金估计量公式,即可得到
将结果代入克里金估计方差,即可得到
因此0号点的泛克里金估计值为14.813,泛克里金方差为5.402。
